Seja a=b. Então,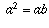 
. Somando-se um mesmo valor em ambos os lados não altera a igualdade, logo 
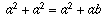. Assim, 
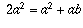. Adicionando-se agora 2ab a cada lado da equação, resulta em 
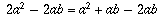. Assim, 
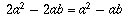, que pode ser escrito como 
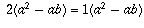. Cancelando o termo 
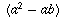de ambos os lados na equação, resulta que 1=2.
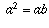. Somando-se um mesmo valor em ambos os lados não altera a igualdade, logo 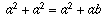. Assim, 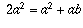. Adicionando-se agora 2ab a cada lado da equação, resulta em 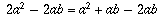. Assim, 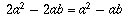, que pode ser escrito como 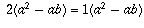. Cancelando o termo 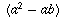de ambos os lados na equação, resulta que 1=2.
6 comentários:
Creio que percebeste isso, mas o termo que cancelaste (e que aliás vinha se repetindo no percorrer da equação) vale zero, o que, me parece, invalida o resultado final, já que uma multiplicação por zero não é de se menosprezar. Que um zero é igual a dois zeros todo mundo sabe. Perante o zero, somos todos iguais!
Muito bem. Chama-se a isto de uma prova falaciosa. Há o dedo da Neusa na descoberta do erro da prova? Se não, parece que tu tem um olho muito bom para problemas matemáticos (falo isto supondo que tu, como um homem das letras, não é treinado em álgebra).
Não há o dedo da Neuza na descoberta, ela está de viagem, cuja volta estou aguardando a fim de dar a mesma dica que te dei: ver o Quem somos nós.
De fato não sou assim tão treinado em álgebra, mas convenhamos que a matemática tem seu aspecto filosófico: tenho lido muita filosofia, ajuda. Mas nesse caso, especificamente, contribuiu a leitura de um texto recomendado na Fabico, Lógica e Filosofia da Linguagem (1892), de Frege, no capítulo Sobre o Sentido e a Referência.
Afinal a matemática também é uma linguagem.
Como curiosidade, vou deixar o começo deste capítulo mencionado no próximo post.
Já assisti o What The Bleep do We Know?. Não tinha me dado conta de que era o mesmo filme. É que eu assisti faz um tempo, em um DVD pirata. As maravilhas modernas, ó filme não está nem pronto e já está disponível para assistirmos no conforto de nossa casa.
Mais do que filosofia, aquilo lá é pura lógica.
E há quem diga que matemática, mais do que uma linguagem, é a linguagem na qual o universo está escrito.
É... se a=b, a^2 = ab e a^2 - ab eh igual a zero! Você multiplica ambos os lados por zero, o que dá em zero = zero, uma solução válida...só que aí vc divide ambos os lados por zero (a^2-ab) o que é impossível. Não se pode dividir um número por zero.
Geralmente essas fórmulas com soluções absurdas usam uma divisão por zero disfarçada para obter tais resultados.
Postar um comentário